선형회귀
*변수간 연관성: 상관계수
상관계수는 변수간 공분산을 각각의 표준편차의 곱으로 나눠준 결과값
코사인 값가 비슷하다
두 벡터간 공유하는 정보가 얼마인지에 대한 측면에서 벡터의 내적과 상관계수는 같은 개념이라 보면된다
*선형회귀: y=β0+β1x1+β2x2+…+βnxn+ϵ
변수간 더하기로 이루어진 세상
-explanatory modeling: x y 관계에 대해 설명하기 위해
-predictive modeling: 미래에 들어올 관측지 y 값을 x 값으로 예측하기 위해
*ei=yi−y^i
실제 측정값과 예측값의 차를 잔차라 한다
*최소제곱측정

min t(e)e로 도 표현 가능
최소제곱측정에서 나온 식을 편미분하여 기울기와 절편을 찾아낸다.
*선형대수 연습
lm(formula, data)함수를 이용하면 앞에서 배운 이론을 바탕으로 기울기와 절편의 값을 알려준다.
> df = mtcars
> View(df)
> names(df)
[1] "mpg" "cyl" "disp" "hp" "drat" "wt" "qsec" "vs" "am" "gear" "carb"
> fit = lm(df$wt~df$mpg, data = df)
> summary(fit)
Call:
lm(formula = df$wt ~ df$mpg, data = df)
Residuals:
Min 1Q Median 3Q Max
-0.6516 -0.3490 -0.1381 0.3190 1.3684
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.04726 0.30869 19.590 < 2e-16 ***
df$mpg -0.14086 0.01474 -9.559 1.29e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4945 on 30 degrees of freedom
Multiple R-squared: 0.7528, Adjusted R-squared: 0.7446
F-statistic: 91.38 on 1 and 30 DF, p-value: 1.294e-10
> names(fit)
[1] "coefficients" "residuals" "effects" "rank" "fitted.values" "assign"
[7] "qr" "df.residual" "xlevels" "call" "terms" "model"- mtcars 데이터셋을 이용하여 선형 회귀 모델을 만들고 분석한 이 모델은 자동차의 무게(wt)(종속)를 연비(mpg)(독립)를 이용하여 예측하는 것을 시도하고 있다.
- 회귀식: wt=6.04726−0.14086×mpgwt=6.04726−0.14086×mpg
- 회귀 계수(Intercept): 6.04726
- 회귀 계수(mpg): -0.14086
- 회귀식의 표준 오차: 0.30869 (Intercept), 0.01474 (mpg)
- 회귀식의 t-value: 19.590 (Intercept), -9.559 (mpg)
- 회귀식의 p-value: <2×10−16<2×10−16 (Intercept), 1.29×10−101.29×10−10 (mpg)
-cofficient, 각 변수별 계수의 유의확률
-회귀 모델의 R2 값은 0.7528로, 모델이 설명하는 데이터의 분산의 약 75.28%를 설명한다는 것을 의미합니다
-F-통계량(anova)은 91.38이고, 자유도는 1 및 30입니다
-F-통계량(모델의 적합)은 회귀 분석에서 SSR(회귀제곱합)을 SSE(잔차제곱합)으로 나눈 값
------------>이 결과값에서 나온 R과 f통계량이 무엇인지 더 자세히 알아보자
*R^2의 결정계수
sst(평균과 점들간의 차이)=ssr(내가 만든 모델과 평균의 차이)+sse(잔차)
->회귀모델의 적합도를 판단할 수 있는 수치
-r^2은 상관계수 제곱-ssr/sst=1-sse/sst-0~1 사이에 존재
-사용하고 있는 예측과 반응변수의 분산을 얼마나 줄였는지
-y를 예측했을 대 대비 x 정보를 사용했을 때 성능향상 정도
> pred = predict(fit, df)
> df$wt
[1] 2.620 2.875 2.320 3.215 3.440 3.460 3.570 3.190 3.150 3.440 3.440 4.070 3.730 3.780 5.250 5.424 5.345 2.200
[19] 1.615 1.835 2.465 3.520 3.435 3.840 3.845 1.935 2.140 1.513 3.170 2.770 3.570 2.780
> cor(df$wt, pred)^2 #실제값과 예측값의 상관관계
[1] 0.7528328
> summ=summary(fit)
> summ$r.squared
[1] 0.7528328
-r^2값을 구한식이 둘다 같다
*anova분석:분산을 분석한다
아직은 덜 배웠으니 대충하면
-MSR/MSE=F* 즉 F통계량이다
*선형회귀모델 기본 가정
-예측변수와 반응변수 간의 관계가 선형
-오차항의 분산이 동일
-오차항들이 서로 독립
-오차항의 분포가 평균이0인 정규분포
*다중회귀분석 hat matrix 구하기
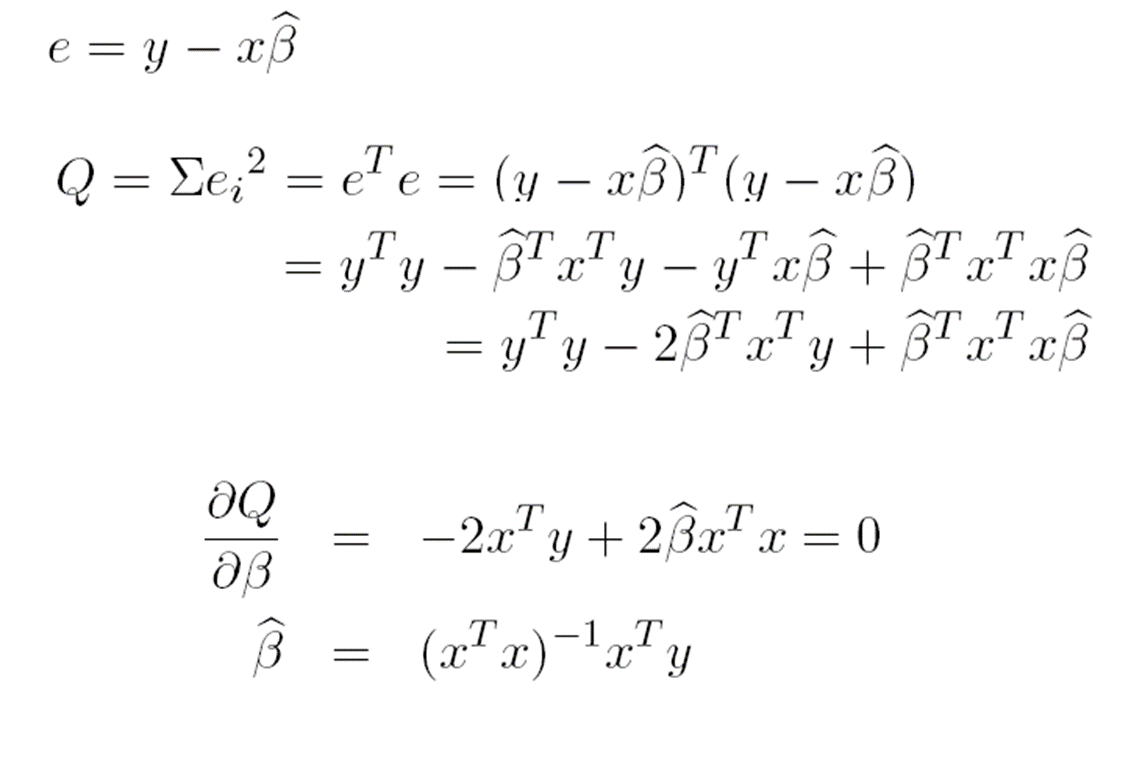
식을 구해왔고 여기에 대입해보면
> df=mtcars
> names(df)
[1] "mpg" "cyl" "disp" "hp" "drat" "wt" "qsec" "vs" "am" "gear" "carb"
> newdf=df[,1:4]
> y=as.matrix(df$mpg)
> x=as.matrix(df[,2:4])
> ones=matrix(1, nrow=nrow(x), ncol=1)
> new_x=cbind(ones,x)
> beta=solve(t(new_x)%*%new_x)%*%(t(new_x)%*%y)
> print(beta)
[,1]
34.18491917
cyl -1.22741994
disp -0.01883809
hp -0.01467933
>
>
> model=lm(newdf$mpg~.,data =newdf)
> summary(model)
Call:
lm(formula = newdf$mpg ~ ., data = newdf)
Residuals:
Min 1Q Median 3Q Max
-4.0889 -2.0845 -0.7745 1.3972 6.9183
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 34.18492 2.59078 13.195 1.54e-13 ***
cyl -1.22742 0.79728 -1.540 0.1349
disp -0.01884 0.01040 -1.811 0.0809 .
hp -0.01468 0.01465 -1.002 0.3250
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.055 on 28 degrees of freedom
Multiple R-squared: 0.7679, Adjusted R-squared: 0.743
F-statistic: 30.88 on 3 and 28 DF, p-value: 5.054e-09위에 식을 적용한 기울기와 절편이 lm함수로 model에서 가져온 기울기와 절편이 같은 걸 볼 수있다.