ANN(artificial neural network)
퍼센트론
신경망/딥러닝 알고리즘의 기원
• 다수의 신호(x)를 받아 하나의 신호(y) 출력
• 입력층과 출력층으로 구성
• 매우 단순하여 실제 문제에 적용되지는 않음 (하지만 개념적으로 중요)
퍼셉트론의 동작원리 ?
• 입력층의 i번째 노드는 변수의 요소 xi를 의미
• 각 변수와 weight를 곱한 다음 다 더함 (weighted sum), 그 다음 활성함수
(activation function) 𝜏를 적용함
• 𝜏라는 계단함수(step function)를 통해 최종 출력(y)는 +1 or -1
퍼셉트론의 W(가중치)는 어떻게 구할까 ?
• OR 문제 (선형 분류가 가능한 경우)
• 퍼셉트론을 활용하여 직선을 만들고 공간을 -1, 1의 영역으로 분할
• 의사결정나무의 목적함수-엔트로피의 최소화 SVM의 목적함수-마진 최대화
• 퍼셉트론 학습(W의 결정)의 목적함수 : Loss Function (손실함수)
• 손실 ? : 분류가 잘못된 정도, 손실이 0 이라는 이야기는 완벽히 분류됨을
의미 ! > 작을수록 좋다! (minimum 문제)
• 즉, 손실함수가 최소가 되는 W를 찾으면 된다.
• 최소가 되는 W는 어떻게 찾지 ? “수치최적화 기법”
수치최적화 기법
• 어떤 함수 f(x)에서 x* 가 최소점이 되기 위해선, x* 지점에서 f(x)의 기울기,
즉, df/dx(함수의 미분값)이 0이라는 조건을 만족해야함 (J(W) = 0, 에러의 변
화가 0, 즉 수렴)
• 미분이 쉬운 문제면 ok, 미분이 불가능 하면 어떻게?
• 시행착오(trial and error)를 반복하여 기울기가 0으로 가는 조건 찾는 법 >
수치최적화 (numerical optimization)
• Newton-Raphson, Gradient Descent 방법 등 (둘다 미분 원리 이용)
• 시작은 항상 random W에서부터
• Gradient Descent는 가장 가파른 방향, 즉, 위치 차(gradient)가 가장 큰 방
향을 골라서 가는 것! > 그러다 보면 언젠간 기울기가 0인 지점에 도달하지않을까
풀이과정-ppt
• 에러가 많이 변할 때는 크게 W를 바꾸고 변화 작을 때는 적게 바꾸고…
• 느낌상, 이렇게만 하면 W는 완벽해질 것 같다…(하지만 현실은 다름 >
update(Backpropagation) 필요)
퍼셉트론의 한계 (AND/OR/XOR)
• XOR문제에 대해서는 단일 선형 분류기로 해결 불가능
• 하지만, 은닉층(Hidden Layer)를 쓴다면 ? > 두개의 선으로 공간을 나누는 효과 발생 !
• 선이 두 개라면 나눌 수 있을 것 같다 > Multi-layer Perceptron
• 왠지, 곡선을 쓰면 나눌 수 있을 것 같다 > Non-linear Activation Function
Multi-layer Perceptron
• 선형분류기(퍼셉트론) 2개를 은닉층을 활용하여 결합할 수 있다
- 새로운 특징 공간 생성 (ex. 1번보단 작고 2번보단 크면 class 1이다)
- 특징 공간에 대해 선형 분류 수행
Activation Function
• 각 layer끼리 정보를 주고 받을 때, 그냥 주지 않는다 (why!!)
- 보다 자연스럽게 자연의 성질을 모델이 받아들이기 위해서 (자연의 비선형성)
• 이때 정보를 변형시키는 함수가 바로 Activation Function(활성화 함수)
• 공간을 선형(step function)/비선형(sigmoid, hyperbolic tangent…)으로
분할 가능 (뭔가 SVM의 커널함수와 역할이 비슷하지 않나?)
ANN등장
중요한 것은, 함수 간 전달시에 출력에 변환을 준다는 것
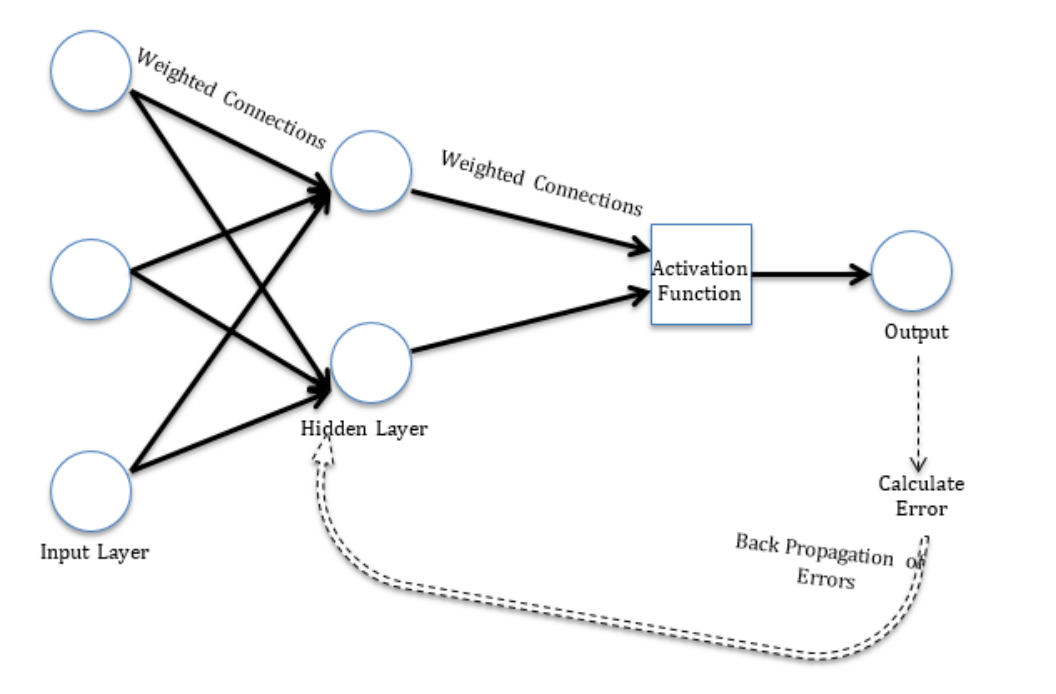
뉴럴 네트워크 모델
'Major > Data Analysis' 카테고리의 다른 글
| Distance & Unsupervised Learning Algorithm (0) | 2024.06.17 |
|---|---|
| Modeling (Artificial Neural Network) & Deep Learning-2 (0) | 2024.06.17 |
| SVM(support vector machine) (0) | 2024.06.17 |
| Decision Tree(의사결정나무) (0) | 2024.06.17 |
| KNN (0) | 2024.06.17 |
