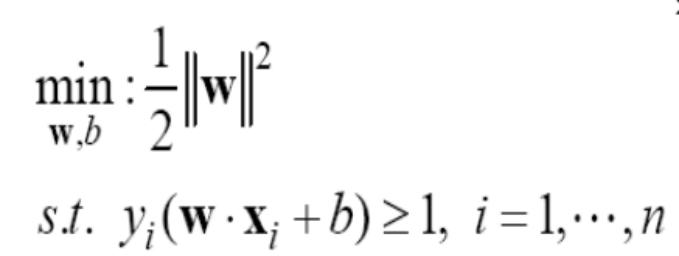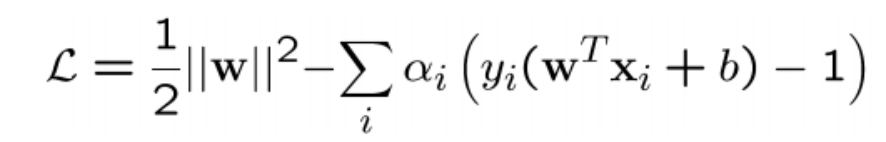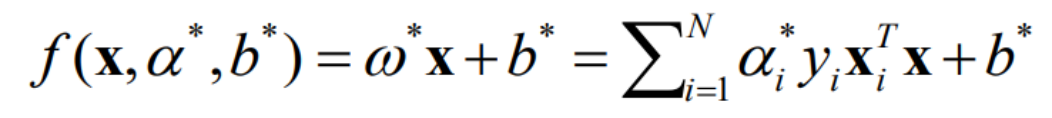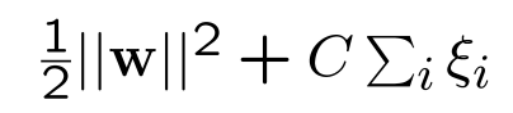Distance ?
• 거리(距離:Distance)는 어떤 사물이나 장소가 공간적으로 얼마나 멀리 떨어져
있는가를 수치로 나타낸 것
• 비슷한 개념으로 유사도/비유사도 존재 (가까우면 비슷하다 멀면 다르다)
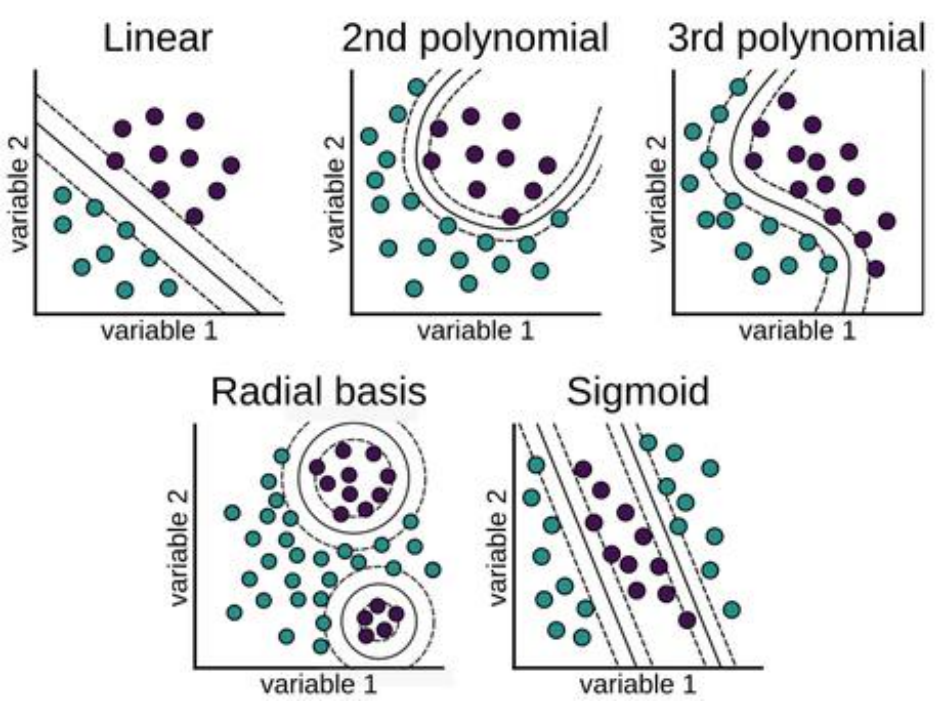
• 머신러닝에서 거리 개념은 매우 다양/유용하게 활용 (ex. SVM에서 마진의 넓
이?/knn에서 가장 근처에 있는 데이터들?)
대표적인 거리들
• 유클리디안 거리(Euclidean Distance : L2 Norm) : 두 점간 차이 제곱하여 모두 더한 값
• 맨하탄 거리 (L1 Norm) : 두 점간 차이의 절대값을 합한 값 (격자 모양의 거리)
• P차 Norm(민코스키 거리) : P = 1이면 맨하탄, 2이면 유클리디안, 무한대일 경우
Chebyshev’s Distance , 일반화된 개념의 수학적 거리 정의임
• 내적 : 벡터끼리 서로 설명하는 수준 (유사도) (밑에 코사인 거리와 유사)
• 코사인 거리(유사도) : 1- 두 벡터의 내적을 각 벡터 크기로 나눈값 (각이 작을수록 값이 작
아짐, 유사함)
• 마할라노비스 거리 : 다변량 통계분포의 특성(관계)를 반영한 거리, 유클리디안 거리를 공
분산행렬로 나눠주는 연산
• 상관관계 거리 : 피어슨 상관계수 응용, 관계가 1 혹은 -1에 가까워질 수록 거리가 작아짐
• 등등등 (데이터간의 유사성/비유사성을 나타내는 모든 것이 거리로 표현 가능)
Euclidean Distance (유클리디안 거리)
• 유클리디안 거리 (L2 Norm)
• 일반적인 다차원 공간에서 두 점 사이의 직선 거리
• 중학교 시절 배운 피타고라스 정리를 기억해보자
• 가장 많이 활용되는 거리 개념, 하지만 변수간의 관계를 고려하지는 못함
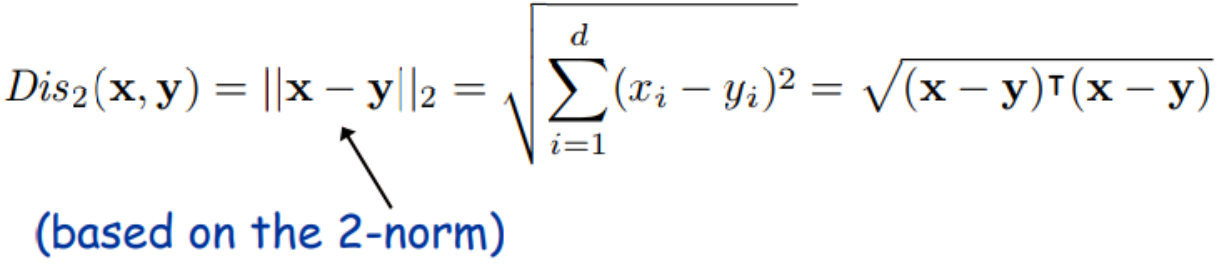
Mahalanobis Distance (마할라노비스 거리)
• 유클리디안 거리를 Covariance Matrix로 나눠준 형태
• 각 변수의 분산으로 나누어 주기에 scale-free(변수별 표준화 됨)
• 변수간의 상관관계 형태를 반영한 거리의 개념으로 다양한 문제에 활용 됨
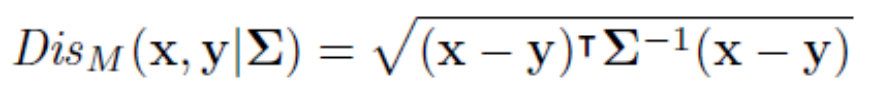
• 다변량 통계학과 머신러닝을 2~3단계 level up 시켜줄 수 있는 Key Algorithm!!
유클리디안 VS 마할라노비스
Center
• 유클리디안 거리는 4개의 점 모두 중심과 거리가 같다
• 어떤 점이 상대적으로 이상해(멀어) 보이는지?
차원의 증가와 거리의 의미
• 거리의 개념은 (특히 유클리디안 거리)는 고차원으로 갈수록 그 효용성이 감소
• 변수의 특징들이 너무 다양하고 많아지는데 반면 단순 크기의 차이(difference)
로는 부족
• 100개의 변수 중 유의(중요)한 변수는 몇 개? 그 중요도를 어떻게 분석에 반영
할 것인가가 중요한 이슈임
• PCA를 통한 거리 계산, 주요 변수 추출, Weight를 부여한 거리의 계산 등 필요
* 각 공간내의 데이터의 개수가 차원 증가로 인해 어떻게 변화하는가 ? (차원의 저주)
Clustering : K-means Clustering Algorithm
Clustering Analysis
Clustering : 관측치(observations)들을 특정 그룹으로 할당(assign)하는 방법론
Clustering Algorithm의 핵심
• 같은 그룹의 데이터는 최대한 유사하게, 다른 그룹간의 데이터와는 최대한 이질적으로 할당하는 것이 good
Clustering을 왜 할까 ?
• 데이터의 패턴을 이해하기 위해 수 많은 데이터들을 특정 그룹으로 요약함
• 데이터를 줄이는 측면에서 feature selection은 열(column)관점의 요약/ clustering은 행(row)관점의 요약
• 데이터의 분포를 다루는 좋은 기반 기술로써 활용 됨 (다른 모델링과 융합가능)
Concept of Clustering Algorithm
• Clustering은 대표적인 비교사학습 (unsupervised learning) 기법 (Y가 없음)
• Distance metrics (ex. Euclidean, Manhattan, correlation, or Mahalanobis
distance) 를 통해 관측치간의 유사성을 연산하여 그룹화
• Hierarchical clustering, k-means algorithm, Self Organizing Map …
계층적 군집화 (Hierarchical Clustering)
• Hierarchical Clustering: 거리 기반의 군집화 알고리즘으로써 비슷한 개체
끼리 계층적으로 그룹화하기 시작하여 최종적으로 한 개의 군집으로 만
드는 알고리즘
• 시각적으로 이해하기 편리함
• 군집수를 사전에 정할 필요가 없음
• 모든 개체들 간(혹은 개체-군집, 군집-군집) 거리가 계산되어야 함 (복잡
도 증가)
• 군집 간 거리계산의 다양한 방법
• Single Linkage: minimum distance
• Complete Linkage: maximum distance
• Average Linkag
K-means Clustering
• 좋은 클러스터링은 ? 같은 그룹끼리는 거리의 합이 최소화!!
• 이것도 결국 ? 또 최적화 문제 !!
• K개의 평균점을 처음 랜덤으로 구하고 각 평균점과 데이터들간의 거리
j 번째 그룹의 평균값)의 합을 최소화 하는 것
• 저번에 배운 미분, 수리최적화, gradient descent 등의 방식으로 풀긴 어
렵다! > 반복적으로 기대값이 최대가 되도록 하는 탐색(search)방법이 적
용되어야 함
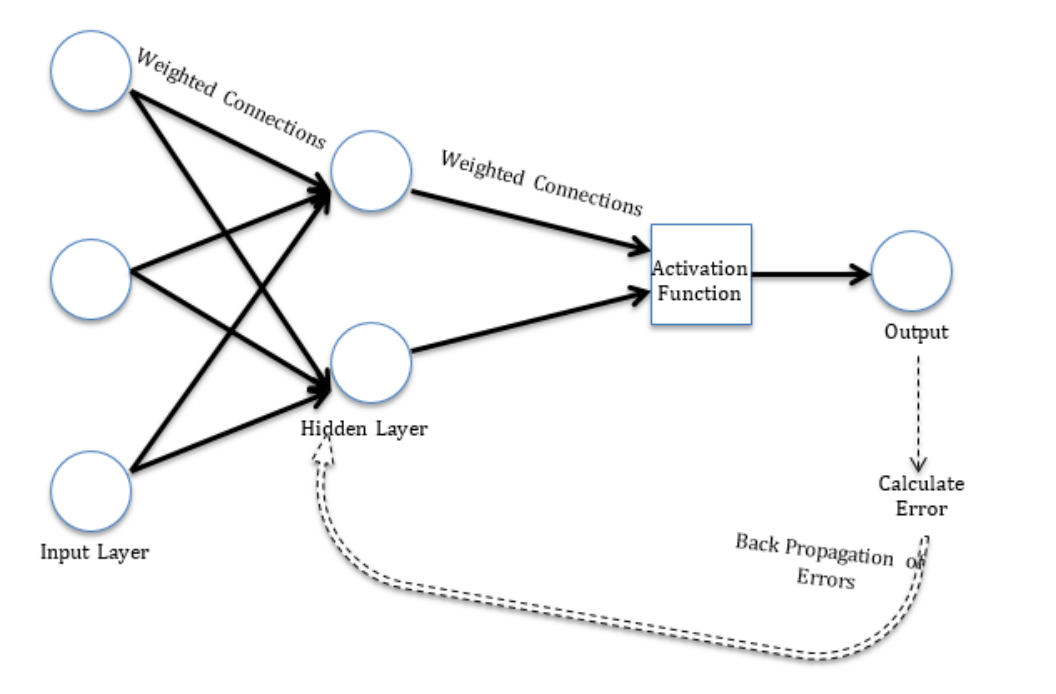
Self-Organizing Map (자기조직화 지도)
• 클러스터링을 위한 인공신경망 (인공신경망중 가장 단순한 형태 중 하나)
• 입력 데이터 > 입력 레이어 > 경쟁 레이어 > 출력으로 구성
• 데이터의 개별 패턴에 상응하는 격자(grid point)에 관측치들을 재배열
• 고차원 데이터에 차원축소 기능과 군집화 동시 수행 (row와 column관점
둘 다 줄임 > 이미지 처리에 높은 빈도로 활용)
• 우선 가중치 행렬(W)를 초기화 함
• Competitive learning : 각 관측치별로 grip point(뉴런이라고 부른다)와의
거리를 산출한 후, 거리값이 가장 작은 뉴런 선택
• 선택된 뉴런과 이웃 뉴런 (격자로 치면 옆에 있는 애들)과의 가중치 (연결
강도) 수정 (수정하는 방법은 gradient descent와 유사, 과거의 w와 실제
데이터와의 차이가 크면 많이 움직이고 작으면 적게!)
• 이러한 연산을 반복하다보면 특정 그리드에 데이터가 몰리게 된다 (군집
효과)
• 그리드 크기는 사용자가 정의해줘야 함
군집화의 성능 평가
• 클러스터링의 이슈 :
- 어떤 거리를 써야 최적일까 ?
- 데이터에 내재된 군집의 개수는 몇 개일까 ?
- 클러스터링이 잘 되었는지 어떻게 평가할까 ?
• 반복실험과 시뮬레이션을 통한 검증을 주로 활용
• Ex. 실루엣 통계량을 통한 성능 평가 (-1 <= silhouette <= 1)
요약 및 의의
• Distance : 데이터간의 비유사도 (거리가 멀수록 이질적, 가까울수록 동질적)
- 마찬가지로 비유사도, 특이한 정도, 통계적 유의도 역시 거리로 표현 가능
• 여러가지 유형의 거리 척도 존재
- Euclidean, Manhattan, Mahalanobis, Minkowski…
- 변수가 많을 경우, 주요 변수의 weight를 어떻게 줄까?
• Clustering : 거리가 유사한 관측치끼리 모아주는 방법
- 같은 그룹내는 최대한 유사하게 다른 그룹과는 최대한 이질적으로…
• K-means Clustering Algorithm
• Self Organizing Map
• 데이터의 row-wise 요약, 다양한 분석의 전처리 기법으로 활용되기도…
'Major > Data Analysis' 카테고리의 다른 글
| Modeling (Artificial Neural Network) & Deep Learning-2 (0) | 2024.06.17 |
|---|---|
| Modeling (Artificial Neural Network) & Deep Learning-1 (0) | 2024.06.17 |
| SVM(support vector machine) (0) | 2024.06.17 |
| Decision Tree(의사결정나무) (0) | 2024.06.17 |
| KNN (0) | 2024.06.17 |